Initial situation
Two types of transformer bushings from my customer were subjected to a special test. It was checked how the bushings would behave in the event of a breakdown inside the insulator and whether the oil in the transformer could catch fire due to the short circuit.
Both types failed the test. I was asked to use simulations to find out the reasons for the failure and to use the knowledge gained to work out improvements.
Realisation
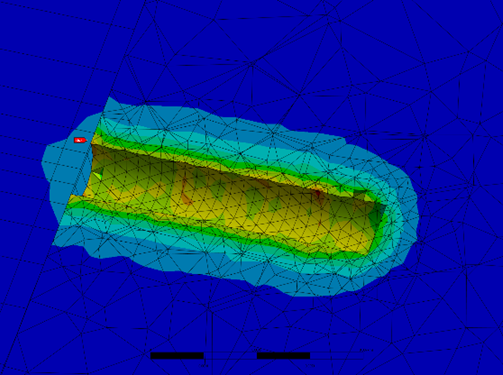
For the simulation of the fast processes during the internal breakdown in the bushing, I have chosen LS-Dyna – an explicit simulation method. I realised the energy deposited by the breakdown in the bushing with an ambient condition coupled with an equation of state of a gas. The idea behind this is that the insulation material in the plasma channel is in a gaseous state.
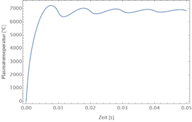
The energy in the plasma channel is represented by the gas temperature. I calculated this with a complex model in LT-Spice, which shows the different temporal phases of the spark resistance in detail. As the processes take place quite quickly and therefore the temperature in the surrounding insulation material hardly rises, a very large temperature reservoir can be assumed. I have taken into account the heat conduction from the plasma to the reservoir with a constant layer thickness. This leads to a plasma temperature of several thousand Kelvin which, however, remains almost constant after the first quarter of the period. This is in agreement with observations in high-energy water breakdowns[1].
I set the temperature curve over time as an input parameter in LS-Dyna for the equation of state. To save time and licence fees, not the entire bushing was modelled but only a section. While I used the Euler formalism for the plasma channel, the components of the bushing use the Lagrangian method. This required a lot of attention to the coupling between the two regimes.
The simulation made it possible to roughly reproduce the observed failure behaviour. This allowed me to suggest measures that would minimise the probability of failure. In addition, I found test parameters within the given text conditions that should make a successful test more likely.
[1] R. Zange – Application-related process model of the conversion of electrical energy into energy of the power sound impulse – Dissertation University of Magdeburg (2000)
Targets and key figures


August – September 2023

Budget 14’000 CHF

Independent project work
Energy technology
Testimonial
Without the cooperation of Mr. Müller-Siebert, we would never have had these valuable results due to a lack of capacity and expertise. He delivered the results in a professional report.”



